حلول رياضيات ثالث ثانوي الفصل الثاني

تحتوي مادة الرياضيات للصف الثالث الثانوي، الفصل الثاني، على مجموعة متنوعة من المفاهيم والتطبيقات المهمة. وتغطي هذه الحلول جميع الموضوعات الرئيسية الواردة في الكتاب المدرسي، بما في ذلك المعادلات والمت不等ات والمثلثات والدوال والمتتاليات.

المعادلات

تتناول هذه الحلول مجموعة واسعة من المعادلات، بما في ذلك معادلات الدرجة الأولى والثانية والمتعددة الحدود. كما توفر طرقًا خطوة بخطوة لحل المعادلات باستخدام مجموعة متنوعة من التقنيات، مثل التحليل والتبديل والتجميع.
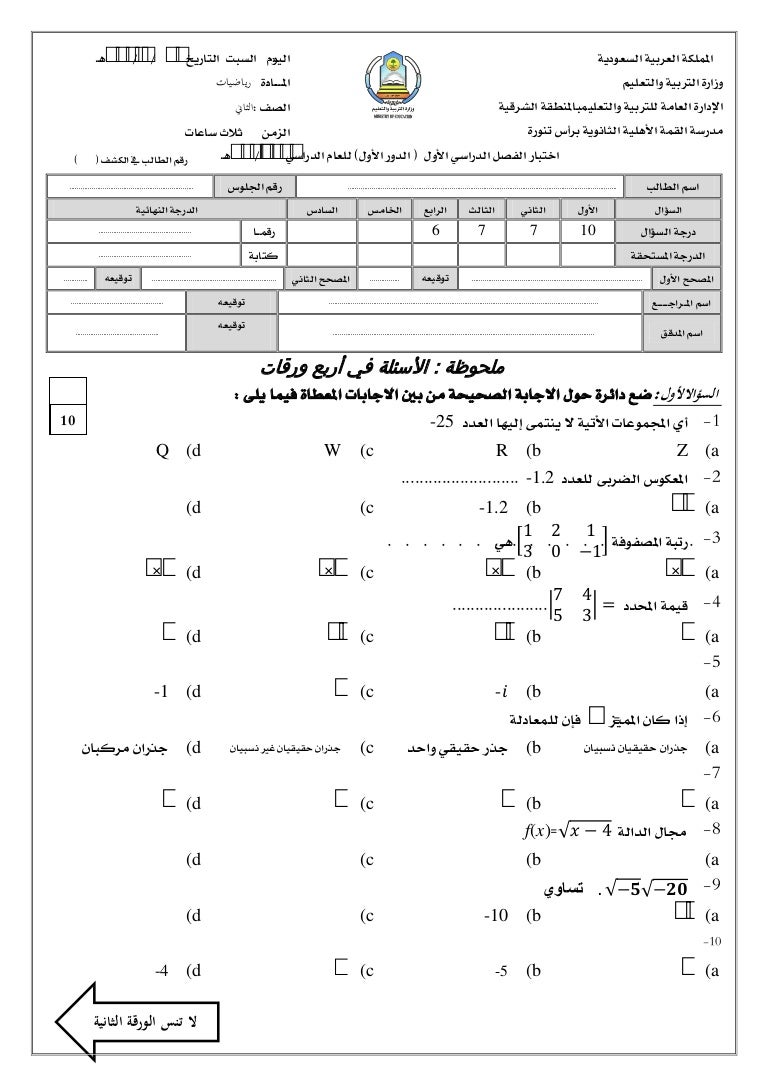
تتضمن الأمثلة:
- حل المعادلة: 2x + 5 = 11
- حل المعادلة التربيعية: x^2 – 5x + 6 = 0
- حل نظام المعادلات:
- 2x + 3y = 10
- x – y = 1
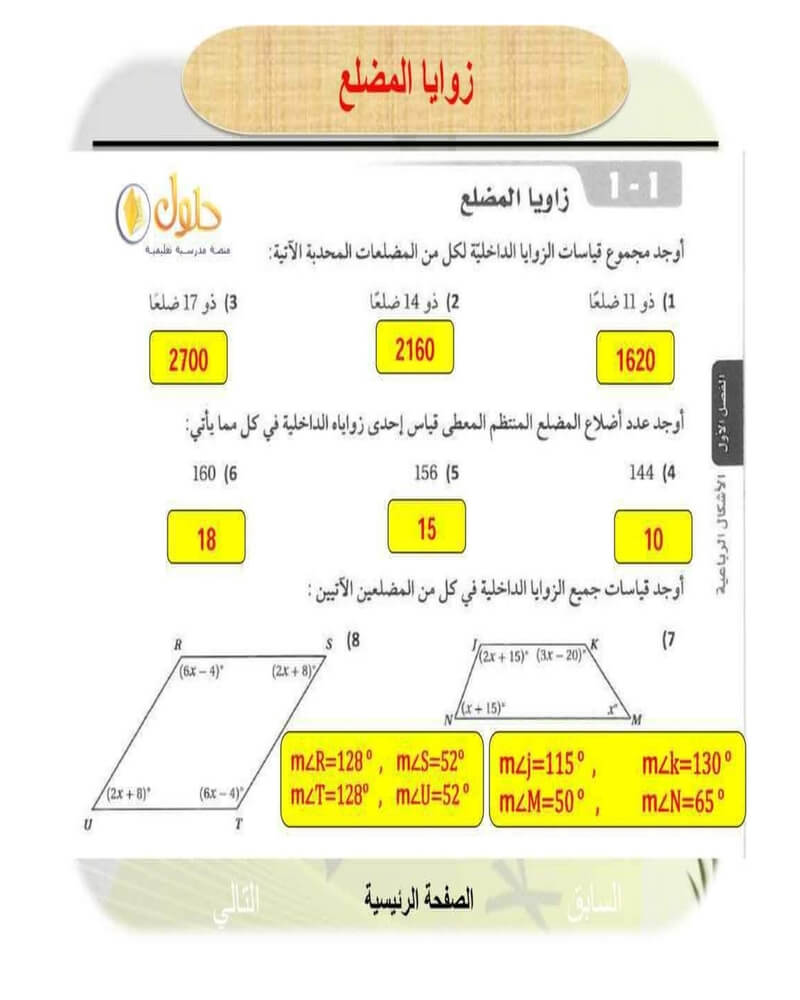
المت不等ات

تغطي هذه الحلول المفاهيم الأساسية للمتفاوتات، بما في ذلك أنواع المتفاوتات المختلفة وخصائصها. كما توفر طرقًا لحل المتفاوتات الخطية والتربيعية والمتعددة الحدود.

تتضمن الأمثلة:

- حل المتفاوتة: x – 2 > 5
- حل المتفاوتة التربيعية: x^2 – 4x + 3 < 0
- حل نظام المتفاوتات:
- x + y > 5
- x – y < 1
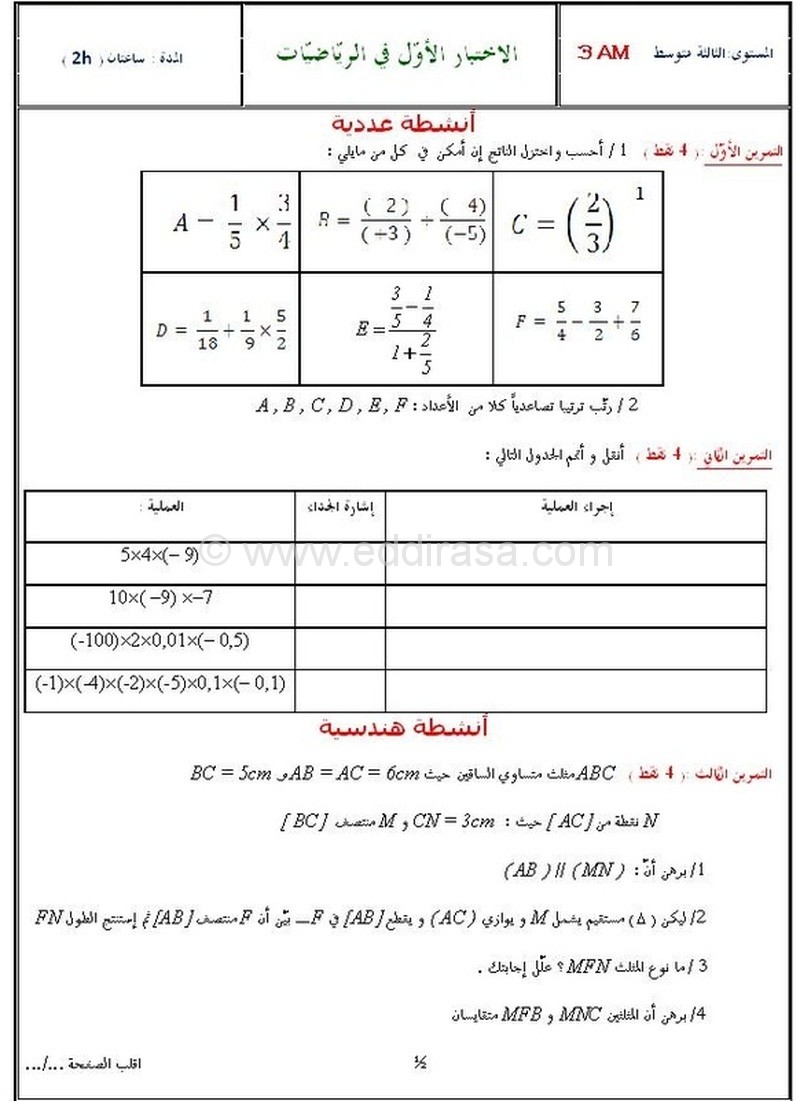
المثلثات

تقدم هذه الحلول فهمًا شاملاً للمثلثات، بما في ذلك أنواع المثلثات المختلفة وخصائصها. كما توفر طرقًا لحل مشاكل المثلثات باستخدام مجموعة متنوعة من التقنيات، مثل قانون الجيب وقانون جيب التمام ونظرية فيثاغورس.

تتضمن الأمثلة:
- إيجاد زوايا مثلث إذا كانت أطوال أضلاعه معروفة
- إيجاد مساحة مثلث إذا كانت أطوال أضلاعه معروفة
- إثبات أن مثلثين متشابهين
الدوال

تغطي هذه الحلول المفاهيم الأساسية للدوال، بما في ذلك أنواع الدوال المختلفة وخصائصها. كما توفر طرقًا لرسم الدوال وتحديد مجالها ومداها. بالإضافة إلى ذلك، تناقش هذه الحلول مفهوم التابع العكسي.

تتضمن الأمثلة:

- رسم الدالة: f(x) = x^2 – 2x + 1
- إيجاد مجال الدالة: f(x) = 1/(x-2)
- إيجاد تابع الدالة: f(x) = 2x + 3

المتتاليات
تقدم هذه الحلول فهمًا لمفهوم المتتاليات، بما في ذلك أنواع المتتاليات المختلفة وخصائصها. كما توفر طرقًا لإيجاد الحدود والاختبارات التقاربية للمتتاليات. بالإضافة إلى ذلك، تناقش هذه الحلول مفهوم المتسلسلات.
تتضمن الأمثلة:

- إيجاد الحد التالي للمتتالية: 1, 3, 5, 7, …
- إثبات أن المتتالية 1/n متقاربة
- إيجاد مجموع المتسلسلة:
- 1 + 1/2 + 1/4 + 1/8 + …

التفاضل والتكامل

تتناول هذه الحلول المفاهيم الأساسية للتفاضل والتكامل، بما في ذلك قواعد التفاضل والتكامل. كما توفر طرقًا لحل مشاكل التفاضل والتكامل باستخدام مجموعة متنوعة من التقنيات، مثل القاعدة الأسية وقاعدة السلسلة وقاعدة حاصل القسمة.

تتضمن الأمثلة:
- إيجاد مشتق الدالة: f(x) = x^3 – 2x^2 + 1
- إيجاد تكامل الدالة: f(x) = sin(x)
- إيجاد مساحة المنطقة الواقعة تحت منحنى الدالة: f(x) = x^2

التطبيقات

تغطي هذه الحلول مجموعة متنوعة من التطبيقات للرياضيات في مجالات مثل العلوم والهندسة والاقتصاد. وتوفر حلولًا لمشاكل واقعية تتطلب استخدام المهارات والمفاهيم الرياضية التي تمت دراستها في الفصل.

تتضمن الأمثلة:

- نمذجة حركة جسم باستخدام معادلة حركية
- استخدام الهندسة لإيجاد مساحة وحجم جسم
- استخدام الجبر لحل مشكلة اقتصادية

الخاتمة
توفر حلول الرياضيات للصف الثالث الثانوي، الفصل الثاني، للطلاب فهمًا شاملاً للمفاهيم والمفاهيم الرياضية الأساسية. من خلال حل هذه الحلول بعناية، يمكن للطلاب تحسين مهاراتهم في حل المشكلات واكتساب الثقة في قدرتهم على تطبيق الرياضيات في مجموعة متنوعة من المجالات.