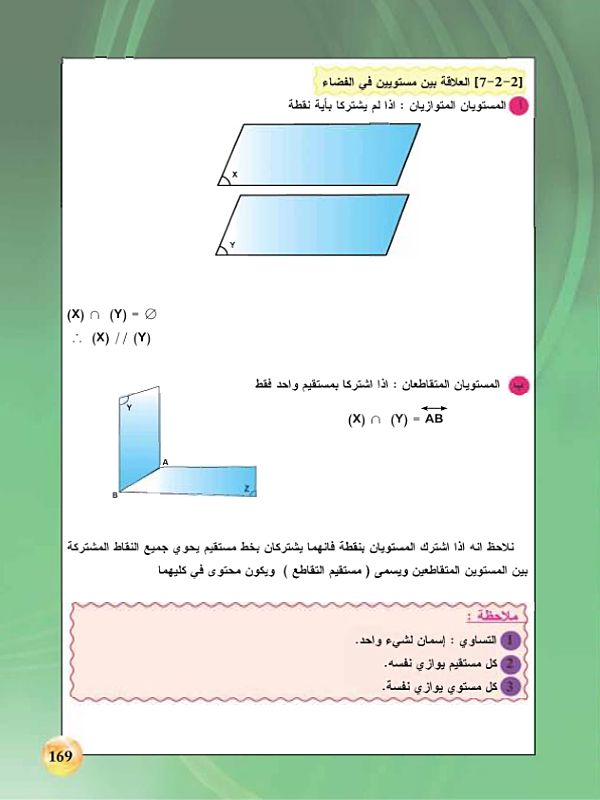
المستقيمان المتقاطعان يحددان مستوى
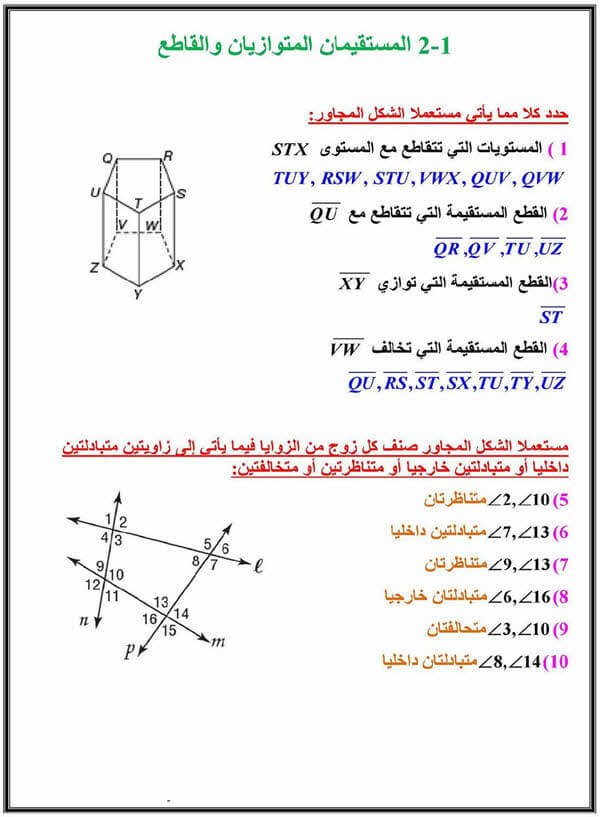
المستوى هو سطح ثنائي الأبعاد يمتد إلى ما لا نهاية في اتجاهين. يمكن تحديده بواسطة ثلاث نقاط غير متوازية أو مستقيمان متقاطعان.
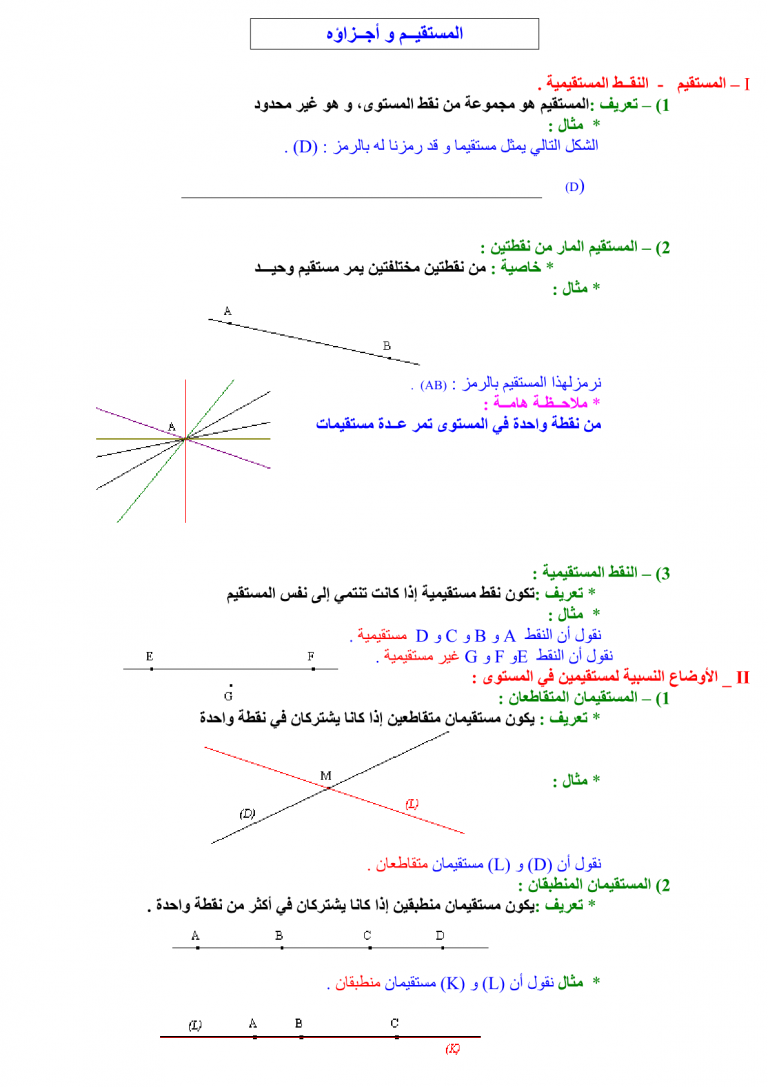
تعريف المستقيمان المتقاطعان
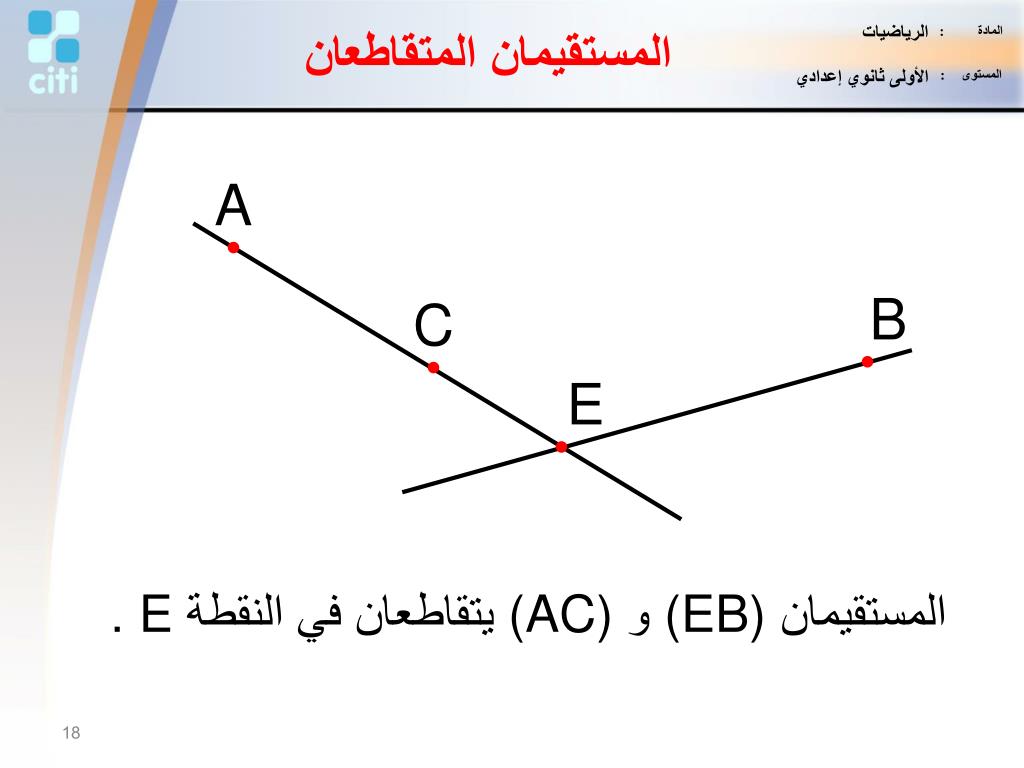
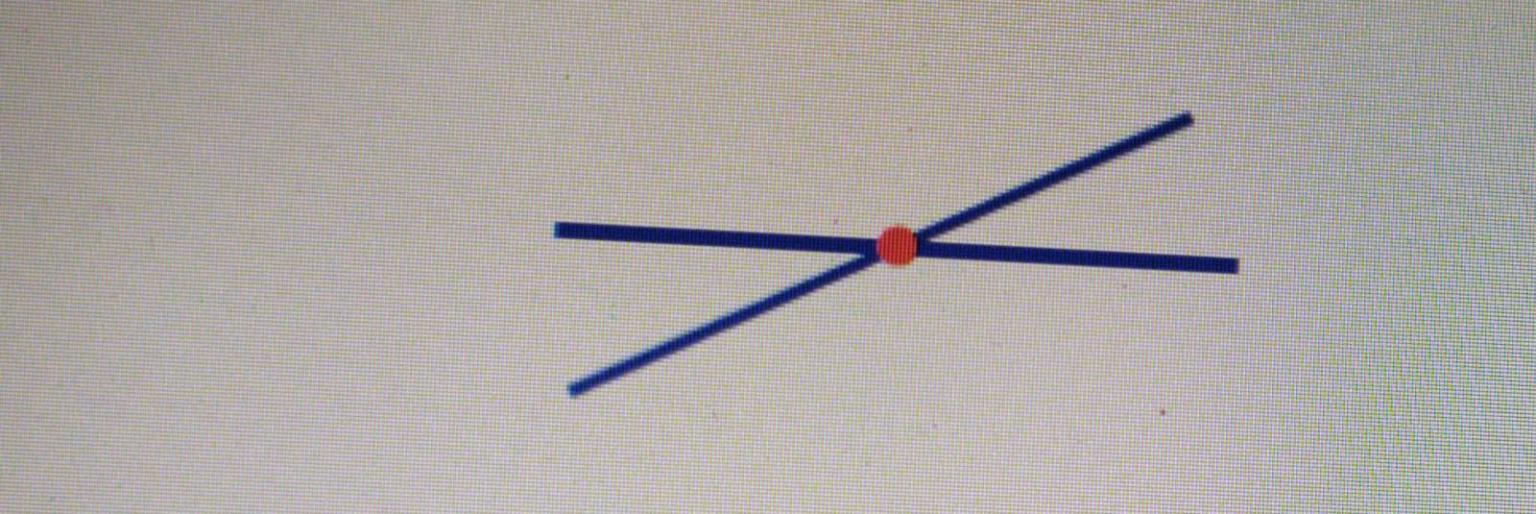
المستقيمان المتقاطعان هما مستقيمان يلتقيان في نقطة واحدة. النقطة التي يلتقيان عندها تسمى نقطة التقاطع.

كيف يحدد المستقيمان المتقاطعان مستوى

عندما يتقاطع مستقيمان، فإنهما يحددان مستوى. هذا المستوى هو المستوى الذي يحتوي على كلا المستقيمين. يمكن تصور الأمر على أنه لوح من الورق به خطان مرسومان عليهما يتقاطعان عند نقطة واحدة. يمثل اللوح مستوى، والخطان يمثلان المستقيمين المتقاطعين.
خصائص المستوى الذي يحدده المستقيمان المتقاطعان
للمستوى الذي يحدده المستقيمان المتقاطعان عدة خصائص مهمة:

1. يمتد إلى ما لا نهاية في اتجاهين

بما أن المستوى سطح ثنائي الأبعاد، فإنه يمتد إلى ما لا نهاية في اتجاهين. وهذا يعني أنه لا يوجد له حواف أو نهايات.

2. يحتوي على جميع النقاط الموجودة على المستقيمين المتقاطعين
كل نقطة تقع على أحد المستقيمين المتقاطعين تقع أيضًا على المستوى الذي يحددانه. وهذا يعني أن المستوى يحتوي على جميع نقاط المستقيمين.

3. محدد فريدًا بواسطة المستقيمين المتقاطعين

المستوى الذي يحدده المستقيمان المتقاطعان محدد فريدًا بواسطة هذين المستقيمين. أي مستوى آخر يحتوي على هذين المستقيمين هو نفس المستوى.
تطبيقات المستقيمان المتقاطعان يحددان مستوى
توجد تطبيقات عديدة للمستقيمان المتقاطعان يحددان مستوى، منها:

1. الهندسة المعمارية

في الهندسة المعمارية، تُستخدم المستويات لتحديد الأسطح والجدران والأرضيات. على سبيل المثال، يمكن تحديد السقف بواسطة مستوى يحدده مستقيمان متقاطعان.

2. الهندسة المدنية

في الهندسة المدنية، تُستخدم المستويات لتحديد الطرق والجسور والمباني. على سبيل المثال، يمكن تحديد الطريق بواسطة مستوى يحدده مستقيمان متقاطعان.

3. الرياضيات

في الرياضيات، تُستخدم المستويات لدراسة الهندسة الإقليدية. على سبيل المثال، يمكن استخدام المستويات لتحديد الأشكال ثنائية الأبعاد مثل المربعات والمستطيلات والدوائر.

خاتمة

المستقيمان المتقاطعان يحددان مستوى هو مفهوم أساسي في الهندسة. له تطبيقات عديدة في مجالات مختلفة مثل الهندسة المعمارية والهندسة المدنية والرياضيات. من خلال فهم خصائص المستويين المتقاطعين يحددان مستوى، يمكننا تحديد الأسطح وحل المشكلات الهندسية.
