التناظر الشعاعي

يُقصد بالتناظر الشعاعي في الرياضيات أنماطًا أو أشكالًا تمتد أو تنعكس من نقطة مركزية. ويُعرف أيضًا باسم التناظر المركزي أو التناظر النقطي. يظهر التناظر الشعاعي بشكل شائع في الطبيعة والفن والرياضيات.

خصائص التناظر الشعاعي
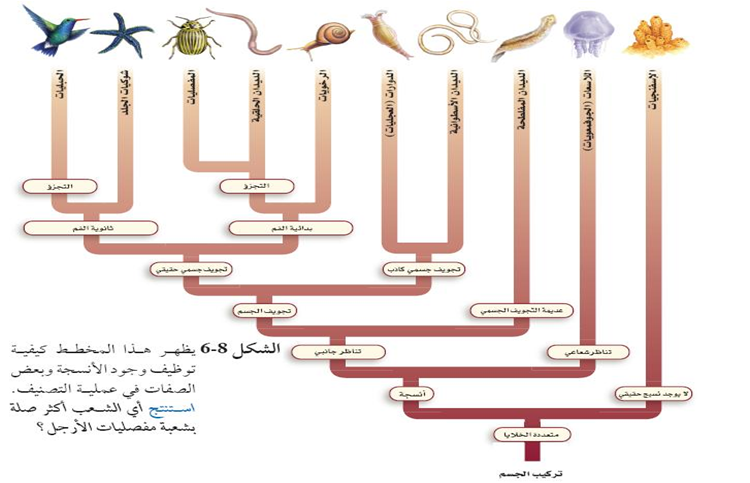
تتميز الأشكال المتناظرة شعاعيًا بالخصائص التالية:


- تتكون من نقطة مركزية واحدة.
- كل نقطة على الشكل على مسافة متساوية من النقطة المركزية.
- عند طي الشكل على نصفين عبر النقطة المركزية، يتطابق النصفان تمامًا.

أنواع التناظر الشعاعي

هناك نوعان رئيسيان من التناظر الشعاعي:

التناظر الشعاعي المنعكس

عندما يُطوى الشكل على نصفين عبر النقطة المركزية، يتطابق النصفان تمامًا. وهذا يعني أن الأجزاء المقابلة من الشكل تتطابق على جانبي النقطة المركزية.
التناظر الشعاعي الدوراني

عندما يدور الشكل حول النقطة المركزية بزاوية معينة، يبدو الشكل متطابقًا مع موضعه الأصلي. وبعبارة أخرى، يُمكن تدوير الشكل حول النقطة المركزية دون تغيير مظهره.

أمثلة على التناظر الشعاعي

توجد أمثلة عديدة على التناظر الشعاعي في العالم من حولنا، منها:

الأزهار

تُظهر العديد من الأزهار، مثل الأقحوان والزنبق، تناظرًا شعاعيًا منعكسًا. حيث تكون بتلات الزهرة متناظرة حول مركز الزهرة.

كعكة عيد الميلاد
تُصمم كعك عيد الميلاد عادةً بشكل دائري مع شموع متناظرة شعاعيًا في الأعلى. يمثل هذا التناظر الشعاعي الرغبة في الاحتفال والتساوي.

دوالة

في الرياضيات، يمكن أن تُظهر الدوال أيضًا تناظرًا شعاعيًا. الدالة التي تكون متماثلة شعاعيًا حول الأصل (0,0) لها القيمة نفسها لـ x سالب وx موجب.

تطبيقات التناظر الشعاعي

يُستخدم التناظر الشعاعي في مجموعة واسعة من التطبيقات، منها:

التصميم

يُستخدم التناظر الشعاعي في التصميم لخلق إحساس بالتناغم والتوازن. ويُمكن رؤيته في العمارة والتصميم الداخلي والفن.

العلوم
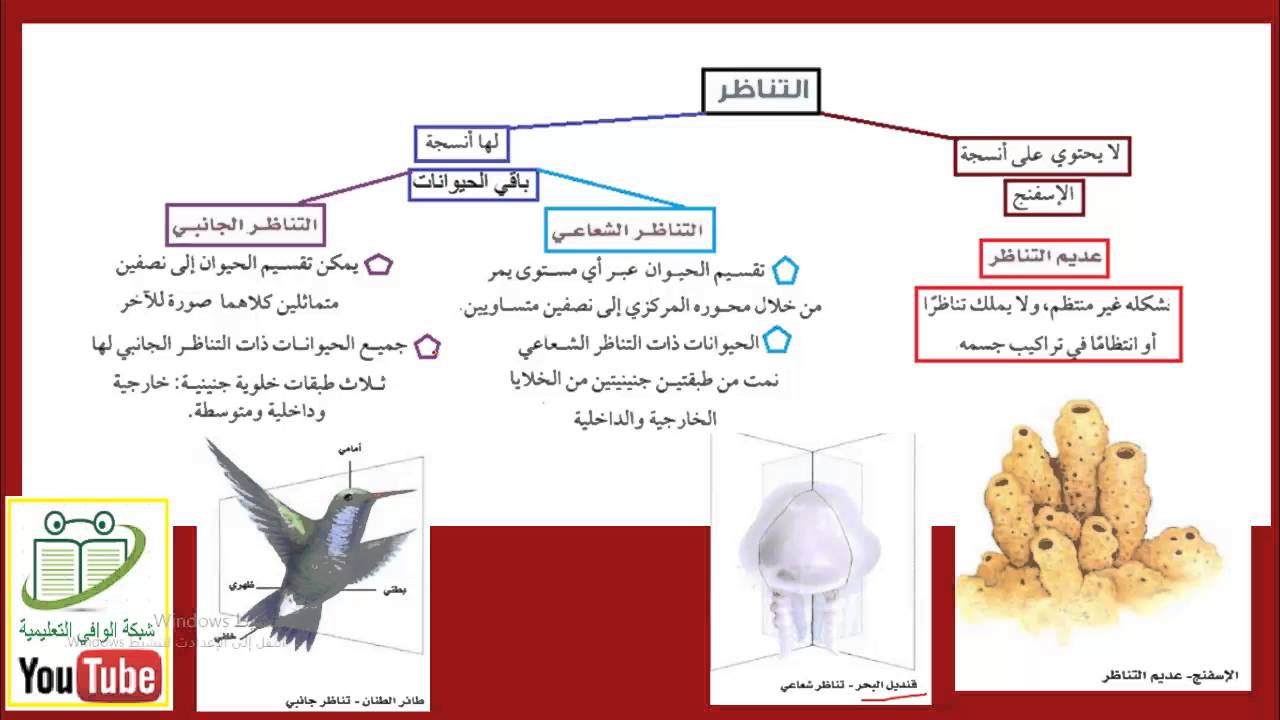
في العلوم، يُستخدم التناظر الشعاعي لدراسة الأنماط والهياكل في الطبيعة. على سبيل المثال، يُظهر جزيء الماء تناظرًا شعاعيًا منعكسًا.

التصنيع

في التصنيع، يُستخدم التناظر الشعاعي لإنشاء منتجات ذات هندسة دقيقة. على سبيل المثال، تُستخدم آلات التصنيع باستخدام الحاسب الآلي (CNC) لإنشاء أجزاء متماثلة شعاعيًا.
خاتمة

يُعد التناظر الشعاعي مفهومًا رياضيًا أساسيًا يتميز بأنماط أو أشكال تمتد أو تنعكس من نقطة مركزية. وهو موجود في الطبيعة والفن والرياضيات ويمكن تطبيقه في مجموعة واسعة من المجالات، بما في ذلك التصميم والعلوم والتصنيع.