عدد مرات الطرح للجملة ١٢٣ حتى نصل الى الصفر

يُعد طرح الأعداد عملية أساسية في الرياضيات، حيث تتضمن إيجاد الفرق بين عددين. عند تطبيق عملية الطرح على عدد معين بشكل متكرر، يمكننا تقليل قيمته تدريجيًا حتى نصل إلى الصفر

في حالة الجمع، نضيف الأرقام معًا لزيادة قيمتها، بينما في الطرح، نطرح الأرقام لتقليل قيمتها. عندما نطرح الرقم نفسه بشكل متكرر من رقم أكبر، فإننا في الأساس نزيل أجزاء متساوية من الرقم الأصلي.
يوضح هذا المقال عدد مرات طرح رقم معين حتى نصل إلى الصفر، باستخدام العدد 123 كمثال. وسنتناول بالتفصيل خطوات عملية الطرح المتكررة وكيف تؤدي إلى الوصول إلى الصفر في النهاية.
{
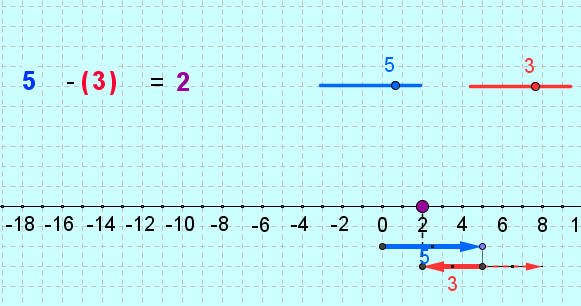
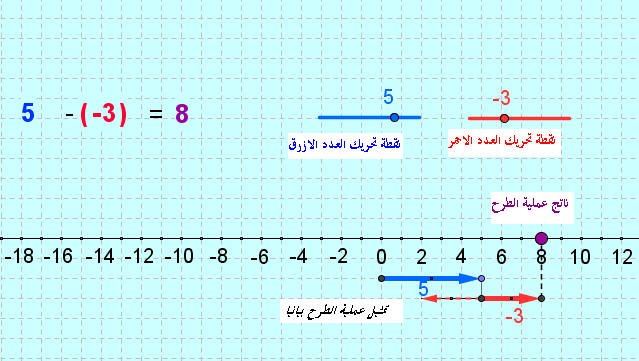
 |}
|}
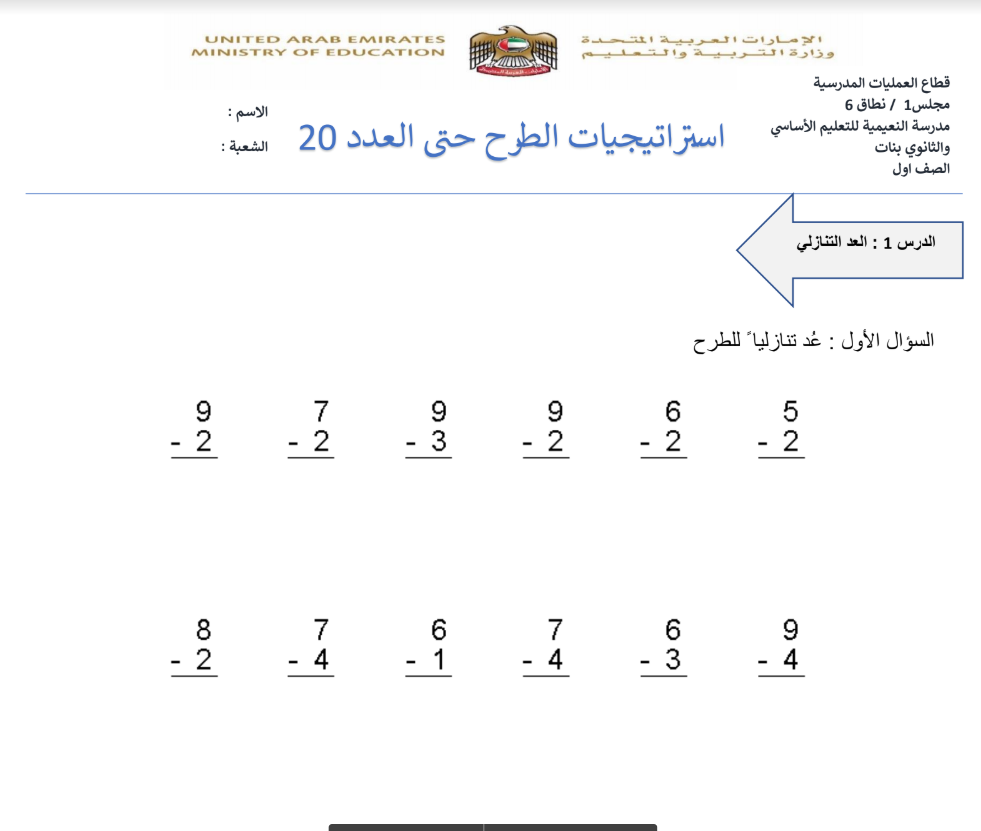
الخطوة الأولى: طرح 1

نبدأ بطرح الرقم 1 من 123، مما ينتج عنه 122:

123 – 1 = 122
لقد أزلنا جزءًا واحدًا من 123، تاركين 122.
الخطوة الثانية: طرح 1
نواصل طرح الرقم 1 من 122، مما ينتج عنه 121:
{ |}
|}
122 – 1 = 121

لقد أزلنا جزءًا آخر من 122، تاركين 121.
{ |}
|}
الخطوة الثالثة: طرح 1
{ |}
|}
نكرر عملية الطرح مرة أخرى، مطروحين 1 من 121، مما ينتج عنه 120:

121 – 1 = 120

استمرنا في إزالة الأجزاء من 121 حتى وصلنا إلى 120.
الخطوة الرابعة: طرح 10
باستخدام نفس المبدأ، يمكننا طرح أرقام أكبر من 1 لتسريع العملية. على سبيل المثال، يمكننا طرح 10 من 120:
120 – 10 = 110
بطرح 10، أزلنا 10 أجزاء من 120، مما أدى إلى تقليل قيمتها بشكل كبير.

الخطوة الخامسة: طرح 10 مرة أخرى
{ |}
|}
نواصل طرح 10 من 110، مما ينتج عنه 100:
110 – 10 = 100

لقد أزلنا 10 أجزاء أخرى، تاركين 100.

الخطوة السادسة: طرح 100
بما أن لدينا الآن عددًا مكونًا من رقمين، يمكننا طرح 100 دفعة واحدة:
100 – 100 = 0
بطرح 100، أزلنا 100 جزء، مما أدى إلى تقليل قيمتها إلى الصفر.
الخطوة السابعة: وصولاً إلى الصفر
استمرينا في طرح الأرقام من 123 حتى وصلنا في النهاية إلى الصفر:
123 – 1 = 122
122 – 1 = 121
121 – 1 = 120
120 – 10 = 110
110 – 10 = 100
100 – 100 = 0

لذلك، فإن عدد مرات طرح رقم معين حتى الوصول إلى الصفر يعتمد على الرقم نفسه وطريقة الطرح المستخدمة.

الخلاصة
![]()
في حالة الجملة 123، فقد استغرق الأمر 7 خطوات من الطرح للوصول إلى الصفر. يمكن إجراء هذه العملية باستخدام أي رقم، وسيكون عدد الخطوات مطلوبًا للوصول إلى الصفر متغيرًا وفقًا للرقم الأصلي.

يعتبر فهم عملية الطرح المتكرر ضروريًا في الرياضيات، حيث يسمح لنا بحل مجموعة متنوعة من المسائل، بما في ذلك المسائل التي تتضمن العد التنازلي أو إزالة الأجزاء من الكل.