خريطة مفاهيم كثيرات الحدود ودوالها

خريطة مفاهيم كثيرات الحدود ودوالها

تُعرف كثيرة الحدود بأنها دوال رياضية يمكن كتابتها على شكل مجموع عدد من الحدود، وكل حد هو حاصل ضرب ثابت في متغير مرفوع إلى قوة صحيحة غير سالبة. ودوال كثيرات الحدود لها العديد من التطبيقات في الرياضيات والعلوم.

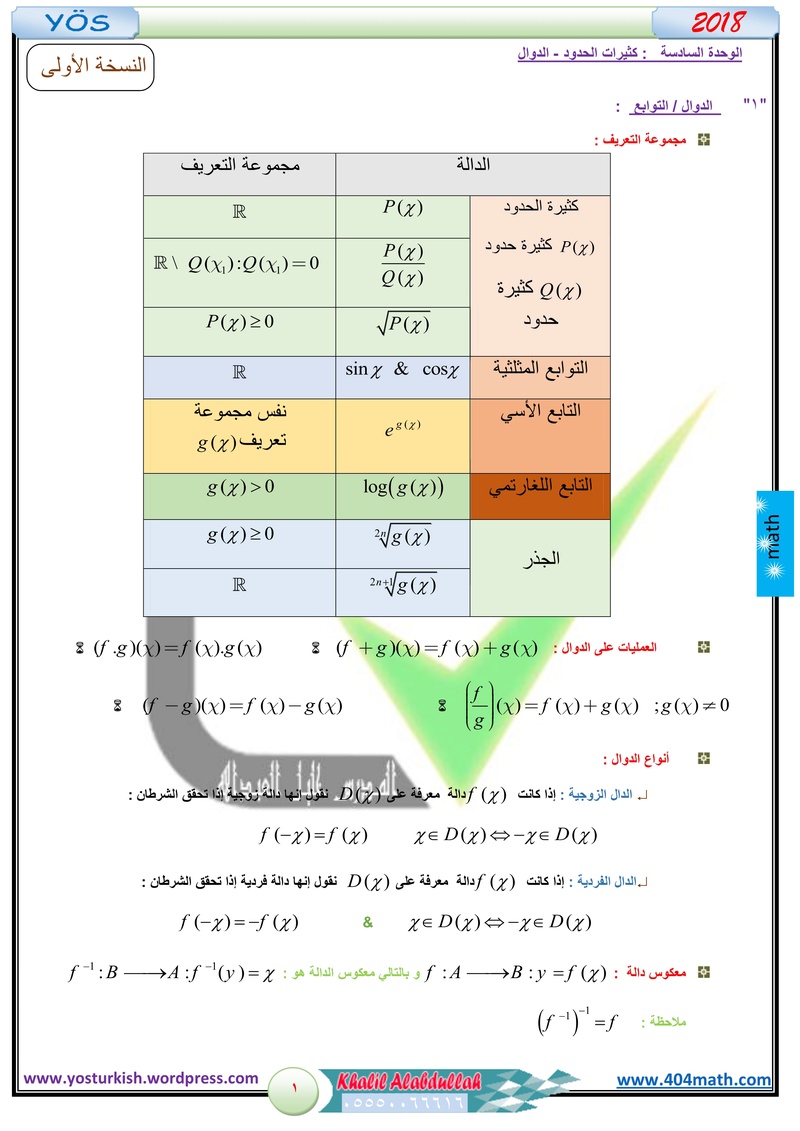
أنواع كثيرات الحدود

{

|}

تصنف كثيرات الحدود حسب الدرجة، وهي أعلى قوة لمتغير في كثيرة الحدود. وإليك أنواع كثيرات الحدود بناءً على الدرجة:

{

|}

*

خطية (الدرجة 1): ax + b

{|}
*

تربيعية (الدرجة 2): ax² + bx + c

*

تكعيبية (الدرجة 3): ax³ + bx² + cx + d

*

رباعية (الدرجة 4): ax⁴ + bx³ + cx² + dx + e

دوال كثيرات الحدود

ترتبط كثيرة الحدود ارتباطًا وثيقًا بدوال كثيرات الحدود، وهي دالة رياضية يمكن تمثيلها بواسطة كثيرة حدود. الرسم البياني لدالة كثيرة الحدود هو منحني يمثل قيم دالة متغير. ويمكن تصنيف دوال كثيرات الحدود أيضًا حسب الدرجة، وترتبط خصائص الرسم البياني ارتباطًا وثيقًا بدرجة كثيرة الحدود.

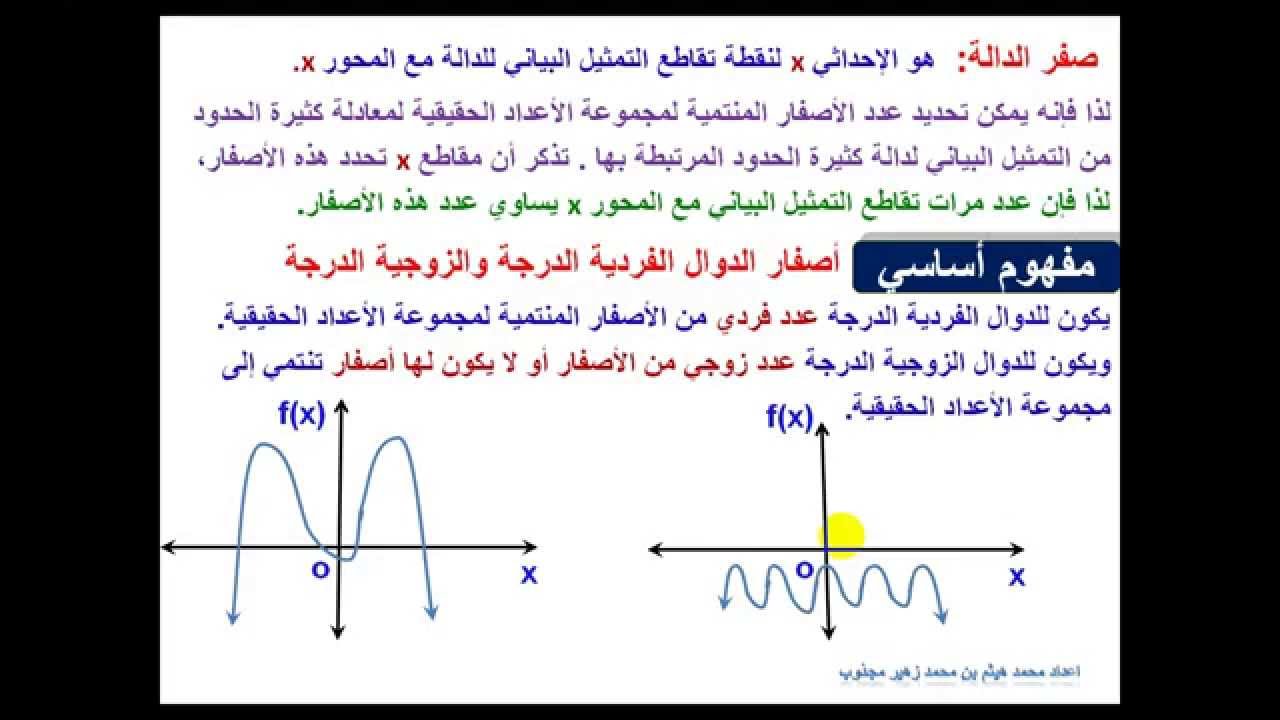
خصائص دوال كثيرات الحدود

تمتلك دوال كثيرات الحدود العديد من الخصائص المهمة، بما في ذلك:

*

الاستمرارية: دوال كثيرات الحدود مستمرة في جميع الأعداد الحقيقية.

*

التفاضل والتكامل: من السهل حساب مشتقات وتكاملات دوال كثيرات الحدود.

*

القيم القصوى والصغرى: يمكن تحديد القيم القصوى والصغرى لدوال كثيرات الحدود عن طريق حساب المشتق.

جذور كثيرات الحدود

جذر كثيرة الحدود هو قيمة المتغير التي تجعل كثيرة الحدود تساوي صفرًا. ويمكن إيجاد جذور كثيرات الحدود عن طريق التحليل أو باستخدام صيغ خاصة، مثل صيغة جذور المعادلة التربيعية.

مبرهنة بقاء العلامة

تنص مبرهنة بقاء العلامة على أن عدد الإشارات المتغيرة في متتالية من معاملات كثيرة الحدود يساوي عدد الجذور الموجبة لكثيرة الحدود عند وضع إشارة الجمع (أو السالب) أمام المتغير.

القسمة الاصطناعية

القسمة الاصطناعية هي طريقة لتقسيم كثيرة حدود على أخرى بشكل أسرع وأسهل من القسمة الطويلة. وتتضمن هذه الطريقة ترتيب معاملات كثيرات الحدود في صف وإجراء عمليات حسابية متتالية.

تطبيقات كثيرات الحدود ودوالها

{|}

تُستخدم كثيرات الحدود ودوالها على نطاق واسع في العديد من التطبيقات، بما في ذلك:

*

النمذجة: يمكن استخدام كثيرات الحدود لنمذجة مجموعة متنوعة من الظواهر الفيزيائية والاجتماعية.

*

التحسين: يمكن استخدام دوال كثيرات الحدود لحل مشاكل التحسين، مثل إيجاد القيمة العظمى أو الصغرى لدالة.

{|}
*

التقريب: يمكن استخدام كثيرات الحدود لتقريب الدوال الأخرى، مثل الدوال المثلثية.

الخاتمة

تُعد كثيرات الحدود ودوالها مفاهيم أساسية في الرياضيات ولها تطبيقات واسعة في العديد من المجالات. ومن خلال فهم خصائص ومفاهيم كثيرات الحدود، يمكن للمرء حل مجموعة واسعة من المشاكل الرياضية والعملية.