تحليل العدد 36 إلى عوامله الأولية

مقدمة :
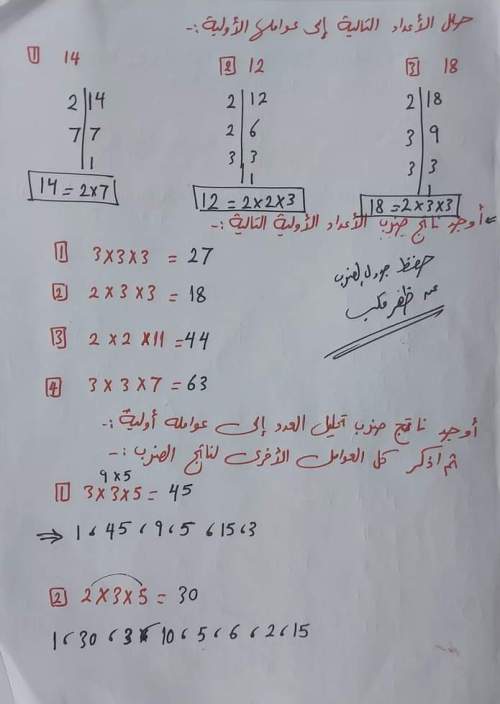
العوامل الأولية هي الأعداد الأولية التي يمكن قسمة عدد ما عليها دون أي باقٍ، وعملية تحليل الأعداد إلى عواملها الأولية مهمة أساسية في نظرية الأعداد ولها تطبيقات عملية في مجالات مختلفة مثل التشفير وتصميم الخوارزميات.

في هذا المقال، سنلقي نظرة متعمقة على تحليل العدد 36 إلى عوامله الأولية، وسنتعلم كيفية إيجاد عوامله بطريقة فعالة ويمكن فهمها.

خطوات تحليل العدد 36 إلى عوامله الأولية :

الخطوة 1: إيجاد العامل الأولي الأصغر

أصغر عامل أولي للعدد 36 هو 2، ويمكننا قسمة 36 على 2 دون أي باقٍ لنحصل على 18.
الخطوة 2: تكرار العملية

نكرر الخطوة 1 مع العدد 18، وأصغر عامل أولي له هو 2 مرة أخرى. ويمكننا قسمة 18 على 2 لنحصل على 9.

الخطوة 3: الاستمرار في القسمة
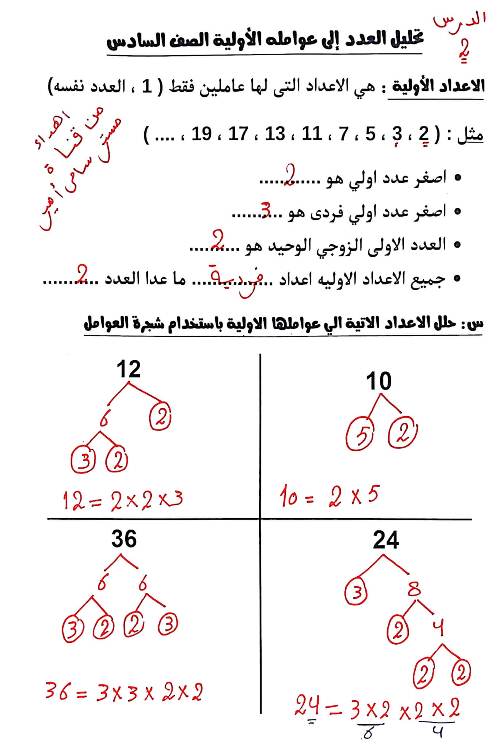
نستمر في القسمة على 2 حتى لا يمكننا ذلك بعد الآن، ونجد أن 9 عدد أولي، وبالتالي فهو العامل الأولي الأخير للعدد 36.

عرض العوامل الأولية :
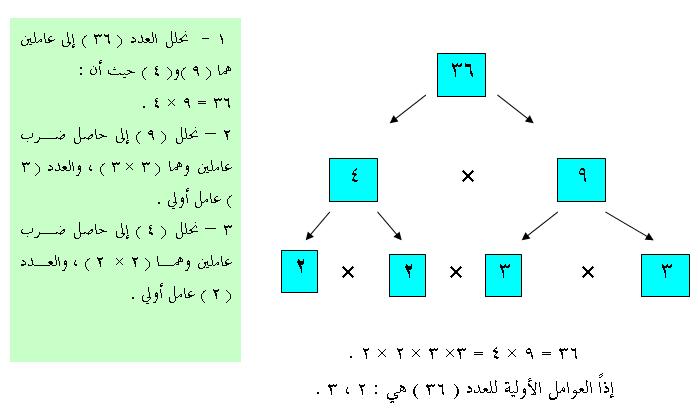
إذن، العوامل الأولية للعدد 36 هي:
36 = 2 × 2 × 3 × 3

ويمكن كتابتها بشكل مضغوط باستخدام أسس الأعداد الأولية:

36 = 22 × 32
تطبيقات تحليل العدد إلى عوامله الأولية :
لتحليل العدد إلى عوامله الأولية تطبيقات عديدة في مجالات مختلفة، منها:
نظرية الأعداد:
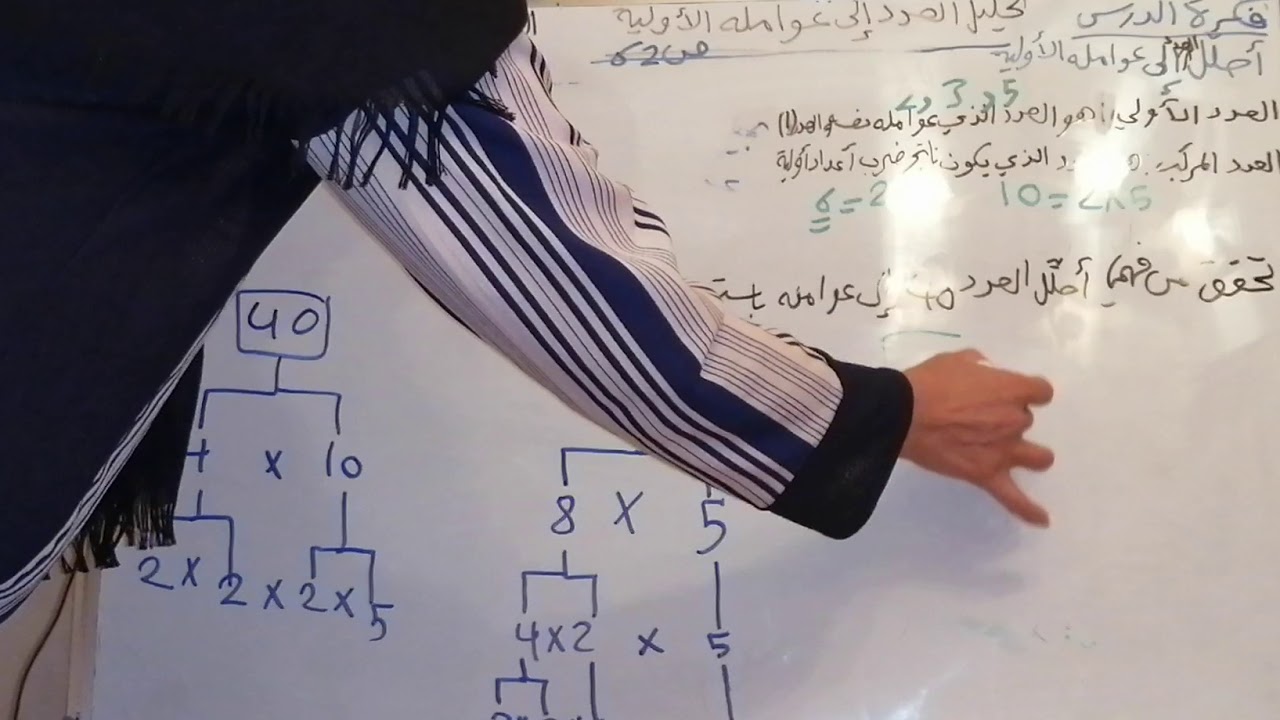
– إيجاد القواسم المشتركة والمضاعفات المشتركة للعدد.
– إثبات نظريات حول قابلية الأعداد للقسمة.

التشفير:

– إنشاء مفاتيح التشفير وفك التشفير الآمنة.

– كسر شفرات التشفير الضعيفة.

تصميم الخوارزميات:

– تحسين كفاءة الخوارزميات الخاصة بعمليات الأعداد الصحيحة.

– إيجاد حلول لكثير من المشاكل الحسابية.

الخصائص الهامة للعوامل الأولية :
لعوامل العدد الأولية خصائص مهمة، منها:

– كل عدد طبيعي أكبر من 1 يمكن تحليله بشكل فريد إلى عوامله الأولية.
– العوامل الأولية لأي عدد هي أولية نفسها.

– عدد العوامل الأولية لأي عدد محدود.

خاتمة :

لقد تعلمنا في هذا المقال كيفية تحليل العدد 36 إلى عوامله الأولية، وهي 22 × 32. كما تعرفنا على خطوات تحليل العدد إلى عوامله الأولية، وتطبيقات هذه العملية في مجالات مختلفة مثل نظرية الأعداد والتشفير وتصميم الخوارزميات.

وتجدر الإشارة إلى أن عملية تحليل العدد إلى عوامله الأولية تعد عملية أساسية في الرياضيات ولها دور كبير في حل العديد من المشاكل الحسابية.