بحث عن تمثيل فضاء العينة

تمثيل فضاء العينة

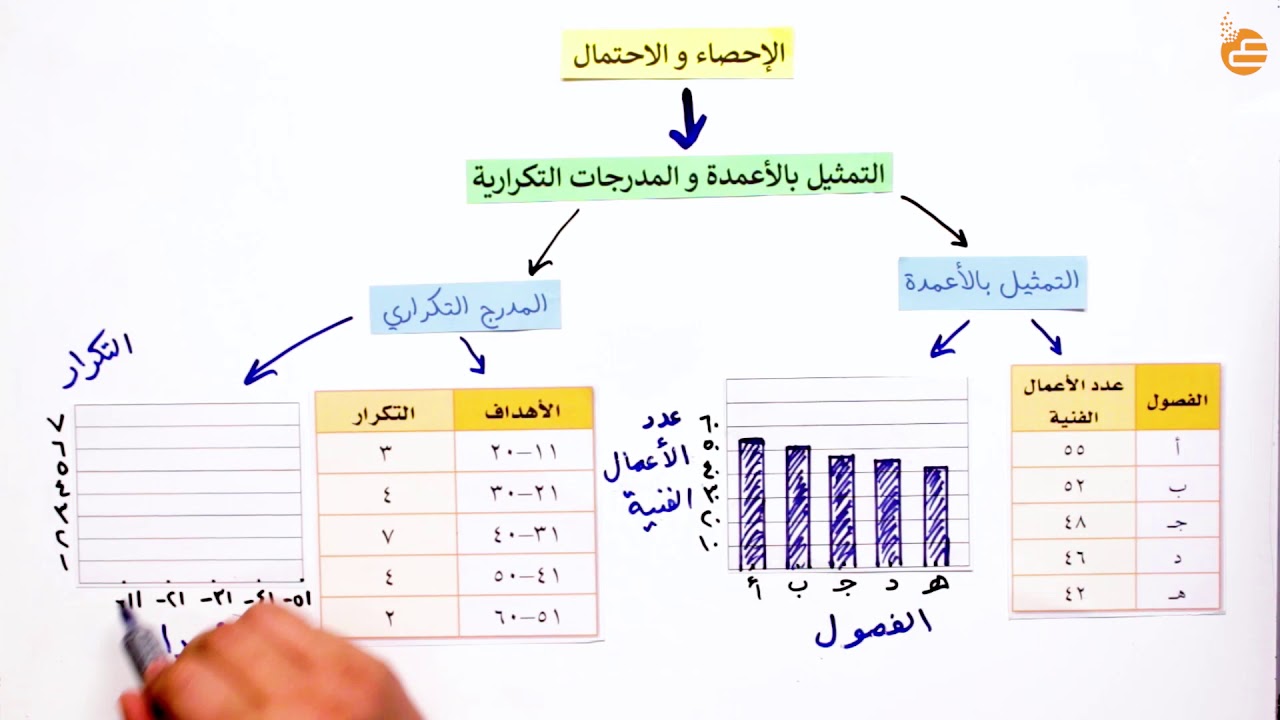
يعتبر تمثيل فضاء العينة خطوة أساسية في نظرية الاحتمالات، فهو يساعد في تحديد جميع النتائج الممكنة لتجربة عشوائية. وفي هذا المقال، سنتعرف على مفهوم تمثيل فضاء العينة وأنواعه وطرق تمثيلها وخصائصها.

مقدمة

{

|}

تمثل فضاء العينة مجموعة جميع النتائج الممكنة لتجربة عشوائية. فعلى سبيل المثال، إذا ألقينا قطعة نقدية، فإن فضاء العينة سيكون رأس، ذيل. وبتعبير آخر، فضاء العينة هو مجموعة النتائج التي يمكن أن تحدث عند إجراء التجربة.
{

|}

أنواع تمثيل فضاء العينة

هناك طريقتان أساسيتان لتمثيل فضاء العينة:

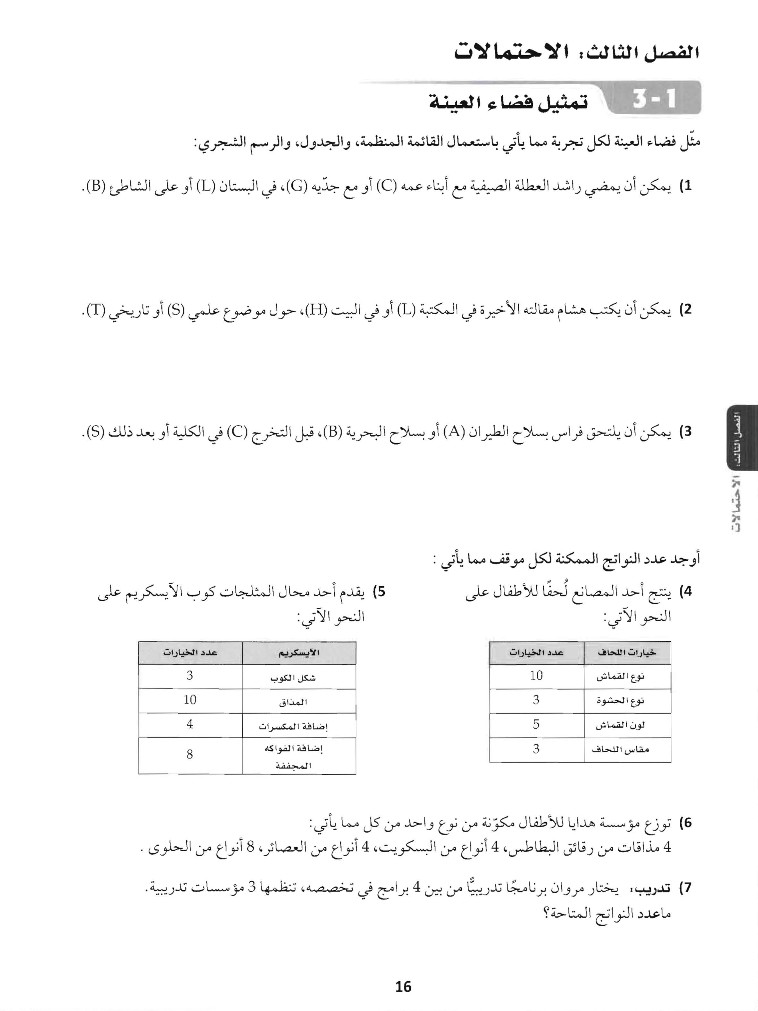
1. التمثيل بالجدول: في هذا النوع، يتم سرد جميع النتائج الممكنة في جدول. فعلى سبيل المثال، إذا ألقينا نردًا، فإن فضاء العينة يمكن تمثيله بالجدول التالي:

نتيجة رمز
——

1 S1

2 S2

3 S3
4 S4
5 S5

6 S6

2. التمثيل البياني: في هذا النوع، يتم تمثيل فضاء العينة باستخدام رسم بياني، مثل مخطط فيني أو شجرة الاحتمالات. فعلى سبيل المثال، يمكن تمثيل فضاء العينة لإلقاء قطعتين من النقود المعدنية باستخدام مخطط فيني كما يلي:

“`

رأس ذيل
——
رأس رأس وذيل (RR) ذيل وذيل (RT)

ذيل رأس وذيل (TR) ذيل وذيل (TT)
“`

خصائص تمثيل فضاء العينة

يتمتع تمثيل فضاء العينة بعدة خصائص مهمة:

1. عدم التكرار: يجب أن تكون جميع النتائج المدرجة في فضاء العينة مميزة وغير متكررة.

2. الشمولية: يجب أن يتضمن فضاء العينة جميع النتائج الممكنة للتجربة.
3. الوضوح: يجب أن يكون تمثيل فضاء العينة واضحًا ومختصرًا.

طرق تمثيل فضاء العينة

هناك العديد من الطرق المختلفة لتمثيل فضاء العينة، اعتمادًا على طبيعة التجربة. فيما يلي بعض الطرق الشائعة:
{|}

1. العد: يعد أبسط طريقة لتمثيل فضاء العينة هو تعداد جميع النتائج الممكنة. فعلى سبيل المثال، إذا ألقينا قطعة نقدية ثلاث مرات، فإن فضاء العينة يمكن تمثيله على النحو التالي:

رأس، رأس، رأس، رأس، رأس، ذيل، رأس، ذيل، رأس، رأس، ذيل، ذيل، ذيل، رأس، رأس، ذيل، رأس، ذيل، ذيل، ذيل، رأس، ذيل، ذيل، ذيل
{|}

2. القواعد الصحيحة: يمكن أيضًا تمثيل فضاء العينة باستخدام القواعد الصحيحة. فعلى سبيل المثال، يمكن تمثيل فضاء العينة لإلقاء نردين باستخدام القاعدة الصحيحة التالية:

S = (s1, t1), (s1, t2), (s1, t3), (s1, t4), (s1, t5), (s1, t6),

(s2, t1), (s2, t2), (s2, t3), (s2, t4), (s2, t5), (s2, t6),

(s3, t1), (s3, t2), (s3, t3), (s3, t4), (s3, t5), (s3, t6),
{|}
(s4, t1), (s4, t2), (s4, t3), (s4, t4), (s4, t5), (s4, t6),
(s5, t1), (s5, t2), (s5, t3), (s5, t4), (s5, t5), (s5, t6),
(s6, t1), (s6, t2), (s6, t3), (s6, t4), (s6, t5), (s6, t6)

حيث S1، S2، S3، S4، S5، S6 تمثل نواتج النرد الأول، وT1، T2، T3، T4، T5، T6 تمثل نواتج النرد الثاني.

3. الحاصل الضربي الديكارتي: يمكن أيضًا تمثيل فضاء العينة باستخدام حاصل الضرب الديكارتي. فعلى سبيل المثال، إذا ألقينا قطعة نقدية وبطاقة من مجموعة من 52 بطاقة، فإن فضاء العينة يمكن تمثيله باستخدام حاصل الضرب الديكارتي التالي:

S = (C, H), (C, S), (C, D), (T, H), (T, S), (T, D)

حيث C و T تمثل وجهي القطعة النقدية، وH و S و D تمثل قلوب وسباتي وكاروه في مجموعة البطاقات.

أهمية تمثيل فضاء العينة

يلعب تمثيل فضاء العينة دورًا مهمًا في نظرية الاحتمالات، فهو يساعد في:

1. تحديد جميع النتائج الممكنة للتجربة.

2. حساب احتمالات الأحداث.

3. إجراء الاستدلال الإحصائي.

خاتمة

يعتبر تمثيل فضاء العينة خطوة أساسية في فهم نظرية الاحتمالات. من خلال تمثيل فضاء العينة بطريقة واضحة ومختصرة، يمكننا تحديد جميع النتائج الممكنة للتجربة وحساب احتمالات الأحداث. وتمثل الطرق المختلفة لتمثيل فضاء العينة أدوات قيمة في تحليل التجارب العشوائية واتخاذ القرارات بناءً على الاحتمالات.