الزاويتان الحادتان في المثلث القائم الزاوية

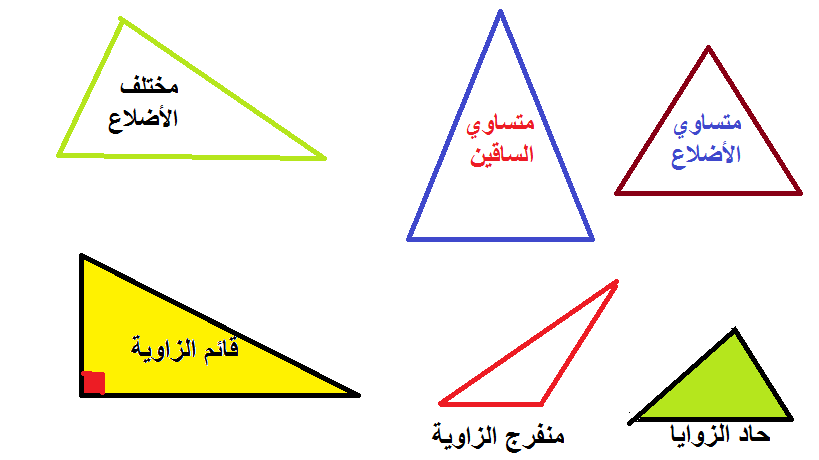
إن المثلث القائم الزاوية هو شكل هندسي ذو ثلاث زوايا ويتميز بكون إحدى زواياه قائمة أي تساوي 90 درجة، بينما تكون الزاويتان الأخريان حادتين أي أقل من 90 درجة. ونظراً لأهمية هاتين الزاويتين الحادتين في خصائص ومبرهنة المثلث القائم، سنتناول في هذا المقال تفصيلاً عن خصائصهما.
مبرهنات الزاويتان الحادتان

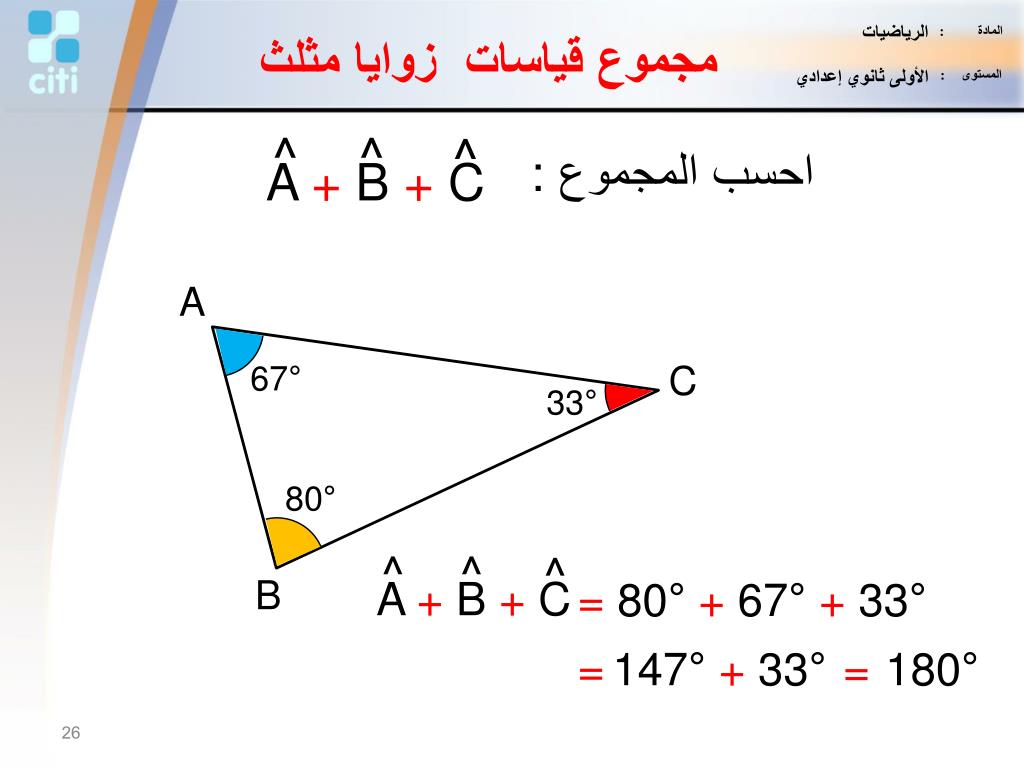
1- مبرهنة مجموع الزوايا: في أي مثلث قائم الزاوية، يكون مجموع الزاويتين الحادتين يساوي 90 درجة.

– البرهان: لنفترض أن لدينا مثلثًا قائم الزاوية؛ الزاوية ABC حيث ∠C = 90 درجة. لنسمح لـ ∠A و ∠B بتمثيل الزاويتين الحادتين.

– بمجموع الزوايا الداخلية للمثلث:

∠A + ∠B + ∠C = 180 درجة
– باستبدال الزاوية القائمة

∠A + ∠B + 90 درجة = 180 درجة
– طرح 90 درجة من كلا الجانبين

∠A + ∠B = 180 درجة – 90 درجة
∠A + ∠B = 90 درجة

2- مبرهنة القاطع والنصف عمودي: إذا رسمنا وترًا عموديًا من أي نقطة على وتر المثلث القائم الزاوية، فإن ناتج ضرب أطوال القطعتين الناتجتين على الوتر يساوي مربع طول الساق المقابلة للنقطة.
– البرهان: لنفترض أن لدينا مثلثًا قائم الزاوية ABC، حيث ∠C = 90 درجة. لنفترض أننا رسمنا وترًا عموديًا BD من نقطة D على الوتر AC. دع BD تقسم الوتر AC إلى جزأين، AD و DC.

– باستخدام نظرية فيثاغورس على المثلثين القائمين الزاوية ABD و BDC
AD^2 + BD^2 = AB^2
BD^2 + DC^2 = BC^2
– ضرب المعادلتين في بعضهما البعض
(AD^2 + BD^2) (BD^2 + DC^2) = AB^2 BC^2
– باستخدام قانون التوزيع
AD^2 BD^2 + BD^3 + BD^2 DC^2 + DC^2 AD^2 = AB^2 BC^2

– إعادة ترتيب المصطلحات
AD^2 DC^2 + BD^2 (AD^2 + DC^2) = AB^2 BC^2

– باستخدام هوية a^2 + b^2 = (a + b)^2

AD^2 DC^2 + BD^2 (AD + DC)^2 = AB^2 BC^2
– بملاحظة أن AD + DC = AC

AD^2 DC^2 + BD^2 AC^2 = AB^2 BC^2

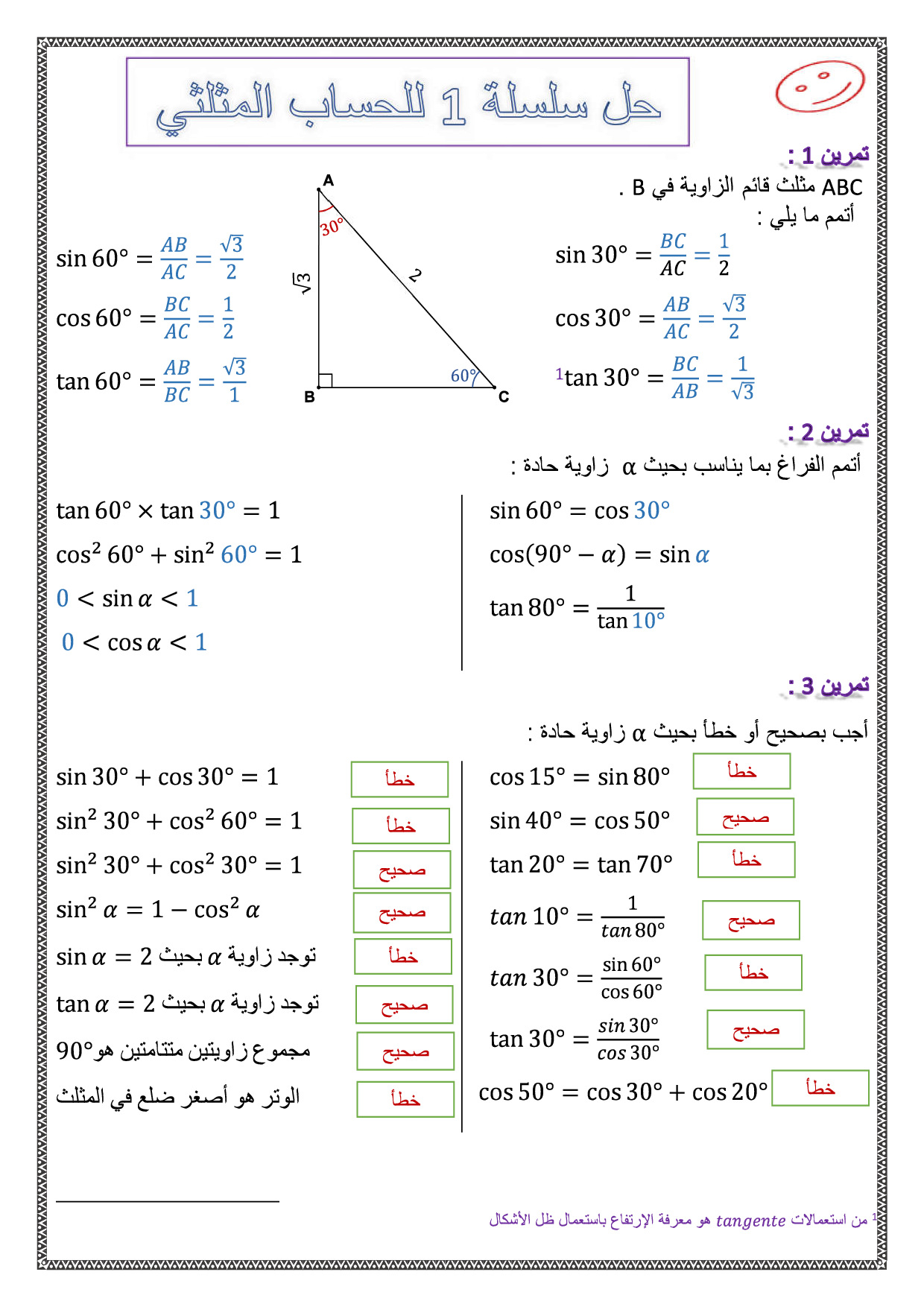
3- مبرهنة تانجر: في المثلث القائم الزاوية، تكون نسبة طول الساق المقابلة للزاوية الحادة إلى طول الساق المجاورة لها مساوية لظل هذه الزاوية الحادة.
– البرهان: لنفترض أن لدينا مثلثًا قائم الزاوية ABC، حيث ∠C = 90 درجة. لنفترض أن a و b هما طولي الساقين المقابل والمجاور للزاوية الحادة ∠A، على التوالي.

– باستخدام تعريف الظل
tan ∠A = مقابل / مجاور = a / b

4- مبرهنة جيب التمام: في المثلث القائم الزاوية، تكون نسبة طول الوتر إلى طول الساق المقابلة للزاوية الحادة مساوية لجيب تمام هذه الزاوية الحادة.
– البرهان: لنفترض أن لدينا مثلثًا قائم الزاوية ABC، حيث ∠C = 90 درجة. لنفترض أن c هو طول الوتر، و a هو طول الساق مقابلة للزاوية الحادة ∠A.
– باستخدام تعريف جيب التمام

sec ∠A = وتر / مقابل = c / a

5- مبرهنة جيب تمام التمام: في المثلث القائم الزاوية، تكون نسبة طول الوتر إلى طول الساق المجاورة للزاوية الحادة مساوية لجيب تمام التمام هذه الزاوية الحادة.

– البرهان: لنفترض أن لدينا مثلثًا قائم الزاوية ABC، حيث ∠C = 90 درجة. لنفترض أن c هو طول الوتر، و b هو طول الساق المجاورة للزاوية الحادة ∠A.

– باستخدام تعريف جيب تمام التمام

csc ∠A = وتر / مجاور = c / b

استخدامات الزاويتان الحادتان
تُستخدم الزاويتان الحادتان في المثلث القائم الزاوية على نطاق واسع في مجالات الهندسة والتطبيقات العملية، بما في ذلك:

1- المساحة: تُستخدم الزاويتان الحادتان لحساب مساحة المثلث القائم الزاوية، والتي تساوي نصف حاصل ضرب الساقين.
2- الارتفاع: يُستخدم مجموع الزوايتين الحادتين لتحديد ارتفاع المثلث القائم الزاوية من خلال الخط المرسوم من الرأس القائم إلى الوتر.
3- حسابات المثلثات: تُستخدم خصائص الزاويتين الحادتين في حل معضلات المثلثات القائمة الزاوية، مثل إيجاد أطوال الأضلاع والزوايا المجهولة.

4- التطبيقات العملية: تُستخدم الزاويتان الحادتان في مجموعة متنوعة من التطبيقات العملية، مثل الملاحة والهندسة المعمارية وقياس الأبعاد.
خاتمة
الزاويتان الحادتان في المثلث القائم الزاوية لهما أهمية كبيرة في خصائص المثلث هذا. من خلال فهم خصائص هذه الزوايا، مثل مبرهنة مجموع الزوايا، ومبرهنة القاطع والنصف عمودي، ومبرهنة تانجر، يمكننا حل مجموعة متنوعة من المشكلات المتعلقة بالمثلثات القائمة الزاوية واستخدامها في التطبيقات العملية.