الدوران بزاوية 90
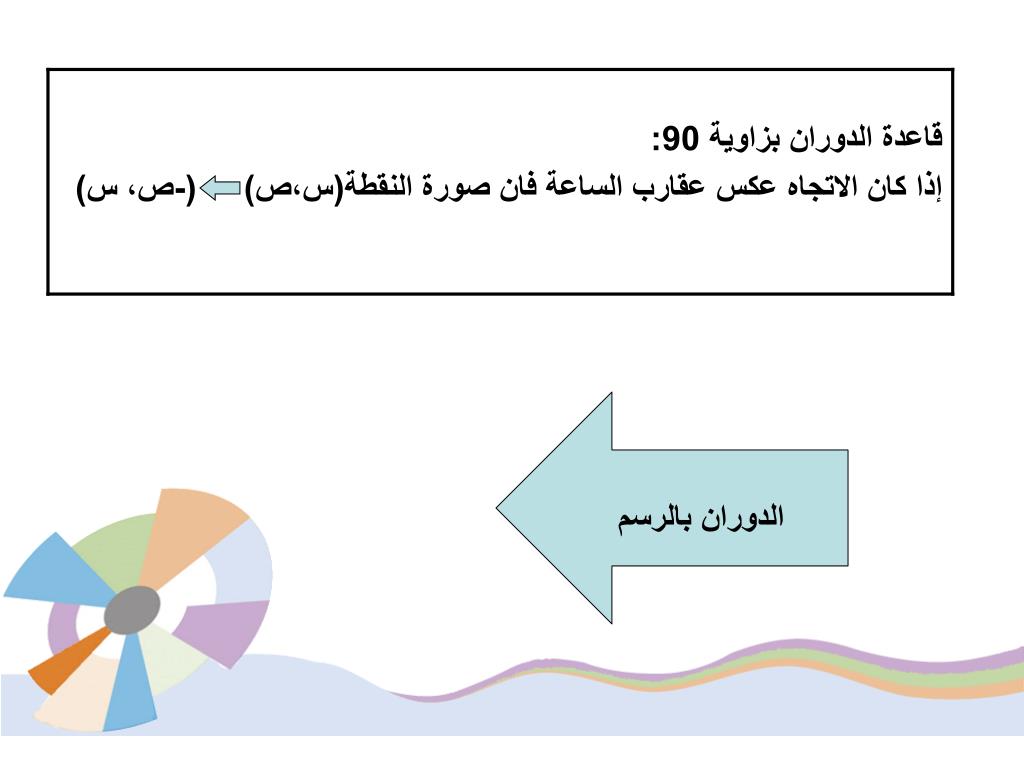
الدوران بزاوية 90 هو تحويل هندسي يحول شكلًا إلى شكله عند دورانه بمقدار 90 درجة حول نقطة ثابتة. وتُعرف هذه النقطة الثابتة بمركز الدوران. يحدث الدوران بزاوية 90 عادة حول أحد المحاور الثلاثة (x و y و z)، وينتج عنه انعكاس للصورة حول هذا المحور.

أنواع الدوران بزاوية 90

* الدوران حول المحور السيني (x): يحول هذا الدوران النقطة (x, y, z) إلى (x, -y, z).
{
 |}
|}
* الدوران حول المحور الصادي (y): يحول هذا الدوران النقطة (x, y, z) إلى (-x, y, z).

* الدوران حول المحور العمودي (z): يحول هذا الدوران النقطة (x, y, z) إلى (y, x, z).

خصائص الدوران بزاوية 90

* يحافظ الدوران بزاوية 90 على المسافات بين النقاط.

* يحافظ الدوران بزاوية 90 على التوازي والتعامد بين الخطوط.

* يحول الدوران بزاوية 90 الأشكال اليمنى إلى الأشكال اليسرى والعكس صحيح.
{ |}
|}
تطبيقات الدوران بزاوية 90

* الرياضيات: يُستخدم الدوران بزاوية 90 في هندسة التحويلات لدراسة الخصائص الهندسية للأشكال.

* الفيزياء: يُستخدم الدوران بزاوية 90 في الميكانيكا الكلاسيكية لوصف حركة الأجسام حول محور ثابت.
{ |}
|}
* الرسومات: يُستخدم الدوران بزاوية 90 في برامج التصميم بمساعدة الكمبيوتر (CAD) لإنشاء نماذج ثلاثية الأبعاد.
* الطب: يُستخدم الدوران بزاوية 90 في التصوير الطبي، مثل الأشعة السينية والتصوير بالرنين المغناطيسي (MRI)، للحصول على صور من زوايا مختلفة.
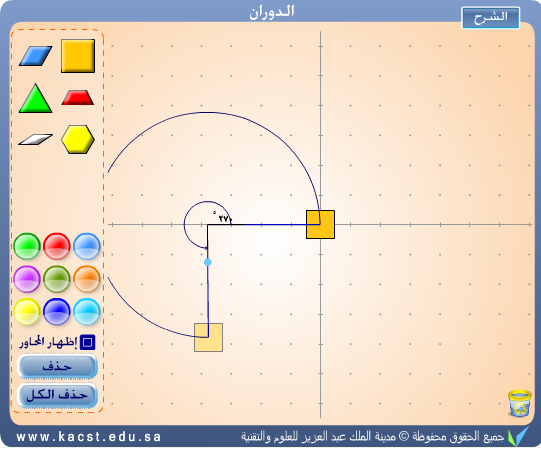
خطوات الدوران بزاوية 90 حول المحور السيني

1. حدد مركز الدوران (x0, y0, z0).

2. احسب الإحداثيات الجديدة للنقطة (x, y, z): (x, -y + 2y0, z).

3. كرر الخطوة 2 لجميع النقاط في الشكل.
{ |}
|}
خطوات الدوران بزاوية 90 حول المحور الصادي

1. حدد مركز الدوران (x0, y0, z0).

2. احسب الإحداثيات الجديدة للنقطة (x, y, z): (-x + 2×0, y, z).
{ |}
|}
3. كرر الخطوة 2 لجميع النقاط في الشكل.
خطوات الدوران بزاوية 90 حول المحور العمودي

1. حدد مركز الدوران (x0, y0, z0).

2. احسب الإحداثيات الجديدة للنقطة (x, y, z): (y, x, z).

3. كرر الخطوة 2 لجميع النقاط في الشكل.

الخاتمة

الدوران بزاوية 90 هو مفهوم أساسي في الرياضيات والفيزياء والرسومات والتطبيقات الأخرى. من خلال فهم خصائطه وتطبيقاته، يمكن استخدامه لحل مجموعة واسعة من المسائل العملية والنظرية.